Parameters¶

The differ object requires several parameters to compute the matching. These parameters are chosen by the user, which makes QBinDiff highly modular.

Distances¶

A distance is used to measure the distance (hence the similarity) between the feature vectors. Choosing a different distance could lead to different behaviors. Note that some features are performing better with a specific distance metric, for example the Weisfeiler Lehman Graph Kernel works best with the cosine similarity.

Most of the distance functions that QBinDiff uses come from Scipy. These distances are computed between two 1-D arrays. Candidate distances are then:

braycurtis
canberra
chebyshev
cityblock
correlation
cosine
euclidean
mahalanobis
minkowski
seuclidean
sqeuclidean

However, some distance are unique in QBinDiff, such as the haussmann distance. This is a experimental new metric that combines the jaccard index and the canberra distance.

Haussmann¶

Formally it is defined as:

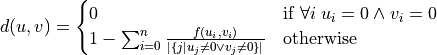
$d(u, v) = \begin{cases} 0 & \text{if } \forall i \; u_i = 0 \land v_i = 0 \\ 1 - \sum_{i=0}^n\frac{f(u_i, v_i)}{ \lvert \{ j | u_j \neq 0 \lor v_j \neq 0 \} \rvert } & \text{otherwise} \end{cases}$

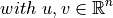
$with\ u, v \in \mathbb{R}^n$

where the function f is defined like this:

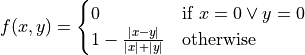
$f(x, y) = \begin{cases} 0 & \text{if } x = 0 \lor y = 0 \\ 1 - \frac{|x - y|}{|x| + |y|} & \text{otherwise} \end{cases}$

Epsilon¶

This is epsilon relaxation. Refer to the Elie Mengin’s thesis to know more about it.

Tradeoff¶

QBinDiff relies on two aspects of a binary/graph: either the similarity (between functions or nodes) or the structure provided by the Call Graph, also known as the topology of the binary.

The similarity is computed with a distance over a linear combination of several features that usually depend on the function attributes. On the contrary, the structure is directly linked on the underlying graphs that come from the binary.

The tradeoff parameter is the weight associated to the importance to give to the similarity or the structure. If the tradeoff is equal to 0, then the algorithm relies exclusively on the topology to diff the binaries. If instead it’s equal to 1, then solely the similarity is used.

Warning

Some features (like ChildNb or GraphCommunities) might also consider the call graph topology, so even if you set the the tradeoff to 1 you still might end up considering the topology to some extent.

Normalization¶

The normalization of the Call Graph is an optional step that aims at simplifying it to produce better results when diffing two binaries.

It simplify the graph by removing thunk functions, i.e. functions that are just trampolines to another function; they usually are just made of a single JMP instruction.

Removing thunk functions has the benefit of reducing the size of the binary, hence improving the efficiency and the accuracy.

Reverse-engineers are usually interested in matching more interesting functions rather than thunk functions, that’s why enabling the normalization pass might be beneficial.

A custom normalization pass can also be set by subclassing QBinDiff and overriding the method normalize().

Warning

In some cases, the normalization may lead to a bug with the BinExport backend. This is due to some specificities of BinExport protobuf file. This may be fixed in the future.

Sparsity¶

If both programs have a larger number of functions, the combinatorial between functions for the similarity might be troublesome (time and memory-wise).

There is usually no need to use the entire similarity matrix as each function will only be similar to a small subset of candidates. Hence, to save memory and to make QBinDiff run faster it’s better to emptying part of that matrix.

You can set the required density of the similarity matrix with the sparsity ratio that goes from 0 to 1:

The closer to 0, the more information is kept. The matrix will be bigger, the matching slower but more accurate
The closer to 1 the less information is kept. The matrix will be smaller, the computation faster but results might be less accurate.

Warning

If your binaries are large (~10k functions) and your RAM is limited, running QBinDiff with a low sparsity ratio may lead to a out-of-memory error. In that case, consider increasing the sparsity ratio (even values like 0.9 or 0.99 are usually perfectly fine).