Metrics¶

pairwise_distances¶

qbindiff.passes.metrics.pairwise_distances(X, Y, metric: Distance = Distance.euclidean, *, n_jobs=None, **kwargs)[source]¶

Compute the distance matrix from a vector array X and Y. The returned matrix is the pairwise distance between the arrays from both X and Y.

In addition to the scikit-learn metrics, the following ones also work with sparse matrices: ‘canberra’

The backend implementation of the metrics rely on scikit-learn, refer to the manual of sklearn for more information:

https://scikit-learn.org/stable/modules/generated/sklearn.metrics.pairwise_distances.html

WARNING: if the metric is a callable then it must compute the distance between two matrices, not between two vectors. This is done so that the metric can optimize the calculations with parallelism.

Parameters:

X – ndarray of shape (n_samples_X, n_features). The first feature matrix.
Y – ndarray of shape (n_samples_Y, n_features), The second feature matrix.
metric – qbindiff.Distance, default=Distance.euclidean The metric to use when calculating distance between instances in a feature array. The implementation of the metric might relybe provided by scikit-learn
n_jobs –
int, default=None The number of jobs to use for the computation. This works by breaking down the pairwise matrix into n_jobs even slices and computing them in parallel.

None means 1 unless in a joblib.parallel_backend context. -1 means using all processors.
**kwargs – optional keyword parameters Any further parameters are passed directly to the scikit-learn implementation of pairwise_distances if a sklearn metric is used, otherwise they are passed to the callable metric specified.

Return D:

ndarray of shape (n_samples_X, n_samples_Y) A distance matrix D such that D_{i, j} is the distance between the ith array from X and the jth array from Y.

haussmann¶

qbindiff.passes.metrics.haussmann(X, Y, w=None)[source]¶

Custom distance that takes inspiration from the jaccard index and the canberra distance. If computes the distance between the vectors in X and Y using the optional array of weights w.

The distance function between two vector u and v is the following: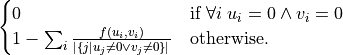

$\begin{cases} 0 & \text{if } \forall i \; u_i = 0 \land v_i = 0 \\ 1 - \sum_{i}\frac{f(u_i, v_i)}{ | \{ j | u_j \neq 0 \lor v_j \neq 0 \} | } & \text{otherwise.} \end{cases}$

where the function f is defined like this: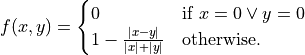

$f(x, y) = \begin{cases} 0 & \text{if } x = 0 \lor y = 0 \\ 1 - \frac{|x - y|}{|x| + |y|} & \text{otherwise.} \end{cases}$

If the optional weights are specified the formula becomes:

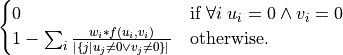
$\begin{cases} 0 & \text{if } \forall i \; u_i = 0 \land v_i = 0 \\ 1 - \sum_{i}\frac{w_i * f(u_i, v_i)}{ | \{ j | u_j \neq 0 \lor v_j \neq 0 \} | } & \text{otherwise.} \end{cases}$

Parameters:

X – array-like of shape (n_samples_X, n_features) An array where each row is a sample and each column is a feature.
Y – array-like of shape (n_samples_Y, n_features) An array where each row is a sample and each column is a feature.
w – array-like of size n_features. The weights for each value in X and V. Default is None, which gives each value a weight of 1.0

Return D:

ndarray of shape (n_samples_X, n_samples_Y) D contains the pairwise haussmann distances.

When X and/or Y are CSR sparse matrices and they are not already in canonical format, this function modifies them in-place to make them canonical.

canberra_distances¶

qbindiff.passes.metrics.canberra_distances(X, Y, w=None)[source]¶

Compute the canberra distances between the vectors in X and Y using the optional array of weights w.

Parameters:

X – array-like of shape (n_samples_X, n_features) An array where each row is a sample and each column is a feature.
Y – array-like of shape (n_samples_Y, n_features) An array where each row is a sample and each column is a feature.
w – array-like of size n_features. The weights for each value in X and V. Default is None, which gives each value a weight of 1.0

Return D:

ndarray of shape (n_samples_X, n_samples_Y) D contains the pairwise canberra distances.

When X and/or Y are CSR sparse matrices and they are not already in canonical format, this function modifies them in-place to make them canonical.